深度学习的崛起几乎完全依赖于反向传播（Backpropagation, BP）算法。BP通过链式法则逐层计算梯度，使得数以百万计的参数能够在训练过程中不断调整。

然而，这一方法在实际应用中存在显著局限,BP需要存储大量中间激活值，导致显存消耗极高，BP依赖的计算模式在类脑硬件或非传统计算架构上难以实现，从生物学角度看，人脑的学习机制与BP存在根本差异，这使得BP在“类脑学习”的探索中显得不够自然。

在这样的背景下，Geoffrey Hinton 在 2022 年提出了 Forward–Forward (FF) 算法。这一方法完全摒弃了反向传播，而是通过两次前向传播来完成学习：一次输入正样本（图像与正确标签），一次输入负样本（图像与错误标签），并利用局部定义的“goodness函数”来更新权重。FF算法的提出不仅是对深度学习训练方式的挑战，更是对生物学启发式学习的一次探索。

FF算法最初仅在全连接网络中得到验证，如何将其扩展到卷积神经网络（CNN）这一图像处理的核心架构，成为亟待解决的问题。

11 月 5 日，《自然》发表研究团队首次系统性地将FF算法应用于CNN 的最新成果，并提出了两种新的空间标签策略，基于傅里叶波的标签与基于形态学变换的标签。这一创新使得卷积层能够在全局范围内捕捉标签信息，避免了传统 one-hot 标签在局部嵌入时的缺陷。

研究由来自德国哥廷根的跨学科团队完成，他们是Riccardo Scodellaro, Ajinkya Kulkarni, FraukeAlves& Matthias Schröter，成员横跨Max Planck Institute for Multidisciplinary Sciences、University Medical Center Göttingen以及 Max Planck Institute for Dynamics and Self-Organization。他们的研究方向涵盖分子影像学、血液学与肿瘤学、放射学以及复杂系统物理学，体现了医学影像、人工智能与复杂系统理论的交叉融合。这种跨学科背景为FF算法在CNN中的应用提供了坚实的理论与实践支撑。

01

工作综述

反向传播虽然是深度学习的基石，但其局限性早已引发广泛关注。BP的存储开销巨大，训练大型模型时显存需求往往是权重存储的数倍。其次，BP在类脑硬件或非传统计算架构上难以实现，限制了其在低能耗计算中的应用。BP与生物神经系统的学习机制差异明显，使得其在“类脑学习”探索中缺乏生物学合理性。

为解决这些问题，研究者提出了多种替代方法。

1.Hebbian学习与对比Hebbian学习：基于“神经元共同激活则连接增强”的局部学习规则，强调生物学动机。

2.平衡传播（Equilibrium Propagation）：在能量模型框架下，通过网络的自由态与约束态差异来驱动学习，连接了Hopfield网络与梯度下降。

3.反馈对齐（Feedback Alignment）、PEPITA等局部学习规则：通过局部误差信号或随机投影来更新权重，避免了逐层反向传播。

4.零阶优化与能量模型：通过两次前向传播的差异来近似梯度，虽然效率较低，但在现代改进下已具备竞争力。

在这一广阔的探索背景下，Hinton提出的 Forward–Forward算法 属于局部学习规则的范畴。它通过正负样本的 goodness 差异来驱动权重更新，避免了反向传播的复杂性。早期应用主要集中在全连接网络，随后扩展到图神经网络、光学神经网络以及类脑硬件实验。然而在卷积神经网络这一主流架构中，FF算法的应用仍是空白。本研究正是填补这一缺口的首次系统性尝试。

02

研究创新点

在这项研究中，最具突破性的贡献是提出了两种全新的空间扩展标签策略，它们直接回应了 Forward–Forward (FF) 算法在卷积神经网络中面临的核心难题。Hinton 在最初的设计中采用的是 one-hot 标签嵌入，即将类别信息编码在图像左上角的几个像素中。

然而这种方式在全连接网络中尚可行，但在卷积神经网络中却存在天然缺陷，卷积核在不同空间位置滑动时，往往无法捕捉到局部嵌入的标签信息，导致网络难以利用标签进行有效学习。

为了解决这一问题，研究团队提出了两种空间化的标签嵌入方法，使得类别信息能够在整张图像中均匀分布，从而保证卷积层在任意位置都能感知到标签信号。

第一种方法是傅里叶波标签。研究者为每个类别生成一组独特的灰度波纹，这些波纹由频率、相位和方向的不同组合构成。通过将这种波纹图像与原始数据进行像素级叠加，标签信息被扩展到整个图像空间。这样一来，卷积核在任何位置都能捕捉到与类别相关的模式，从而避免了局部标签缺失的问题。傅里叶波标签的优势在于其数学上的可控性和全局一致性，能够为网络提供一种稳定的类别信号。

第二种方法是形态学标签。与傅里叶波的全局波纹不同，形态学标签通过对原始图像施加一组确定性的形态学变换来嵌入类别信息，例如膨胀、腐蚀、旋转或其他几何操作。每个类别对应一组独特的变换组合，这些变换会改变图像的结构特征，从而迫使网络在学习过程中关注图像的形态差异，而不是依赖简单的标签模式。形态学标签的优势在于它能有效避免“捷径解”——即网络仅仅依赖标签的简单模式来区分正负样本，而忽视了图像本身的复杂特征。

这两种空间扩展标签策略的提出，直接解决了 CNN 在 FF 框架下的关键问题：如何让卷积核在全局范围内感知类别信息。它们不仅保证了标签信号的空间可达性，还通过不同的机制引导网络学习更深层次的特征。傅里叶波标签提供了全局一致的模式，而形态学标签则强化了对图像结构的关注。两者结合，为 FF-CNN 的训练提供了新的可能性。

从更宏观的角度来看，这一创新点不仅是技术上的改进，更是理念上的突破。它体现了研究团队在类脑学习与卷积架构结合上的深度思考：如果我们希望摆脱反向传播的限制，就必须重新设计标签与数据的交互方式，让网络在前向传播中就能充分利用类别信息。这种思路为未来的类脑计算和低能耗硬件实现提供了重要启示。

03

方法与实现

在针对 MNIST 数据集 的实验中，研究团队设计了一种由三层连续卷积结构组成的网络架构。每一层均采用相同数量的滤波器矩阵，这一参数也是实验中重点考察的超参数之一。值得注意的是，网络中没有引入最大池化层，因为在预实验中发现池化操作会降低整体准确率。

数据流动过程可以概括为：输入图像与其正负标签依次通过三层卷积，每层之后都进行 层归一化（Layer Normalization） 和 ReLU 激活。在每一层中，正负样本的激活差异被用于计算该层的 sigmoid 函数输出，从而形成局部的判别信号。

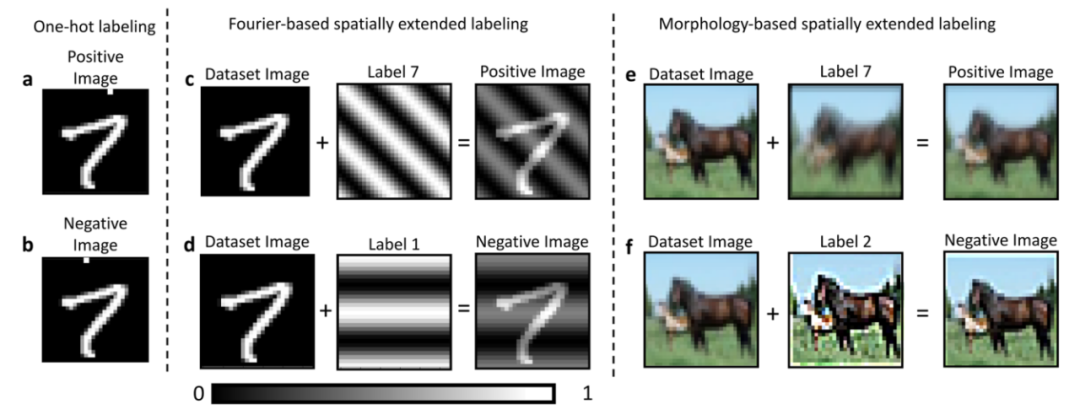
图1：空间扩展标签存在于整个图像中，而一个热编码仅限于左上角区域。对于FF训练，我们需要两个数据集，它们都为图像添加标签。第一行描述了阳性数据集的创建，其中示例图像被正确标记。最下面一行显示了阴性数据集的示例，其中图像与从其他可能标签中随机选择的假标签相结合。我们展示了添加标签的三种方法。（a）和（b）描述了Hinton使用的单热编码：图像顶行的第一个像素用作指示符。在该示例中，设置为1的单个像素的列数对应于目标值。（c）和（d）描述了我们提出的基于傅里叶的技术。每个标签对应于与输入大小相同的图像，但具有特征灰度值波。标签通过逐像素相加的方式包含在图像中。（e）和（f）显示了我们提出的基于形态学的方法。每个标签都与一组独特的变换相关联，这些变换会影响图像形态，迫使网络专注于图像特征。

在数学定义上，优度（goodness） 被设定为该层所有激活值的平方和：

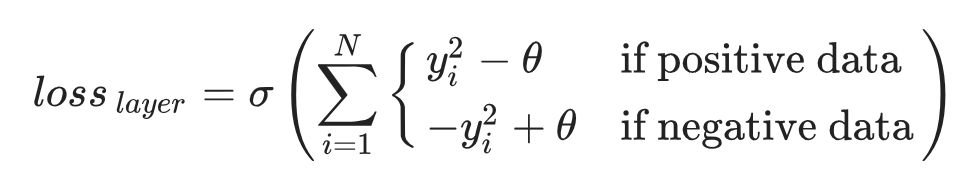
在损失函数设计上，研究者并未采用文献中提出的对称性方案，而是借鉴了其他工作提出的累积网络损失，即通过将各层损失相加来增强层间协作。但与传统做法不同的是，本文排除了第一层的损失。原因在于第一层的激活向量长度本身就能区分正负样本，如果过度依赖这一信息，后续层将无法学习更复杂的特征。通过舍弃第一层的损失，网络被迫依赖相对激活模式，从而在更深层次上提取有意义的特征。这一做法与 Hinton 在原始实现中的选择保持一致。

在训练细节上，团队遵循了两点关键实现。

• 层归一化：对每个激活值进行归一化，使后续层只能利用前一层的模式信息，而非整体范数。

• 学习率线性冷却：在训练周期中途调整学习率，公式如下：
  

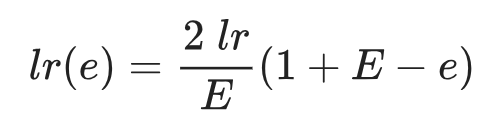
其中，E 表示总训练轮数，e 为当前轮数。

为了分析各层的贡献，研究者定义了基于层的判别损失与准确率。Sigmoid 输出被解释为概率，当值大于 0.5 时，表示该层将图像识别为正样本。通过与真实标签比较，可以得到判别准确率，并进一步计算二元交叉熵损失。

在推理阶段，网络提供了两种方案：

• 线性分类器：除第一层外，每层的 HH 个神经元与一个包含 NN 个节点的分类层全连接，节点数等于类别数。权重通过交叉熵损失训练，这是默认的推理方式。

• 优度评估：每张图像与所有可能的标签组合进行前向传播，计算每个标签的优度值，最终选择优度最大的标签作为预测结果：

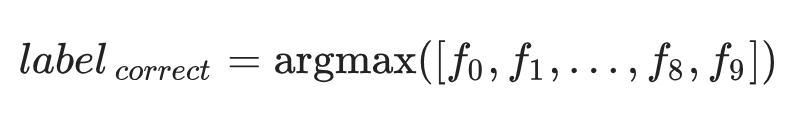
其中，对于每个关联的标签m，其优度表示为

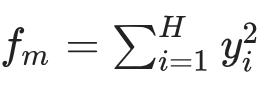
其中H是除第一层神经元之外的所有神经元的数量。

在CIFAR10 与 CIFAR100的实验中，研究团队采用了更深的网络结构。具体而言，网络扩展为六层卷积，并将层归一化替换为 批归一化（Batch Normalization），以提升训练稳定性。这一设计参考了已有文献中的优化方法，同时保持空间扩展标签策略不变。

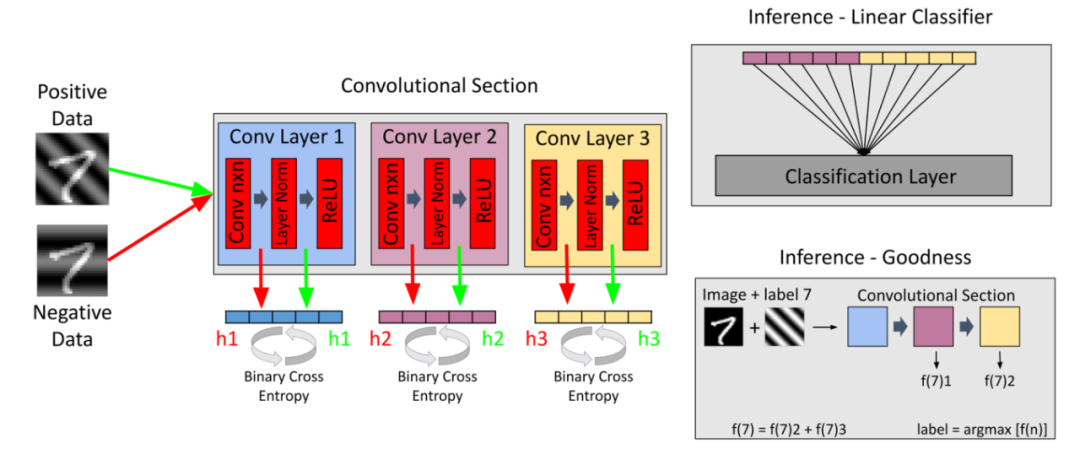
图2：应用于MNIST数据集的FF训练CNN的示意图。正负样本通过三个卷积层进行处理，每个卷积层都经过层归一化和ReLU激活。在每一层，使用正样本和负样本的二元交叉熵计算优度函数。然后，可以通过线性分类器或通过评估所有标签的优度得分来进行最终分类。

这种方法的独特之处在于，它完全摒弃了反向传播的链式梯度计算，而是通过局部 goodness 函数的优化来驱动学习。正负样本的对比机制让网络在没有反向传播的情况下，依然能够逐层提取有意义的特征。

从整体来看，方法与实现部分展示了 FF 算法在 CNN 中的完整落地：通过空间扩展标签保证卷积核能捕捉类别信息，通过 goodness 函数定义训练目标，再通过跨层累计损失与双重推理方式实现分类。这一框架不仅在数学上自洽，也为未来在类脑硬件上的应用提供了可行路径。

04

实验结果与分析

在实验部分，研究团队通过对MNIST、CIFAR10、CIFAR100三个经典数据集的系统测试，验证了 Forward–Forward (FF) 算法在卷积神经网络中的可行性与局限性。结果不仅展示了 FF 与传统反向传播（BP）的性能对比，也揭示了空间扩展标签策略在复杂数据集上的关键作用。

在MNIST数据集上，FF-CNN 的表现几乎与 BP-CNN 持平。采用三层卷积结构（每层 128 个 7×7 卷积核），FF-CNN在测试集上取得了 99.16% 的精度，而BP-CNN 的精度为 99.13%。这表明在简单数据集上，FF 算法完全能够替代 BP。然而，训练动态上存在差异：FF 收敛速度较慢，需要更多迭代才能达到稳定精度，但其内存消耗显著降低，约为 BP 的25–30%。这意味着在硬件受限的场景下，FF 算法具有明显优势。

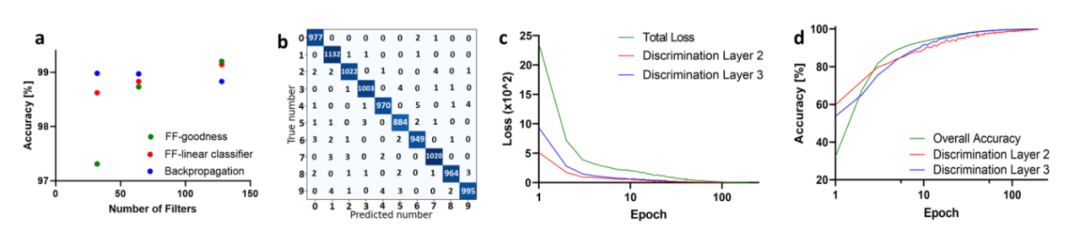
图3：FF训练的CNN架构的最佳MNIST性能与相同架构的反向传播训练的CNN的结果相当。（a）在批量大小为50的200个迭代训练后，根据每层滤波器的数量，为具有三个卷积层的CNN获得的精度值。滤波器大小为7乘以7，学习率分别设置为FF的5x10-5和BP的10-3的最佳值。FF训练的网络使用来自集合1的标签和35%的标签强度K。BP和FF的报告值是从验证数据中收集的。绿色数据点显示了与FF训练网络相关的结果，并使用优度比较进行推理。在这种情况下，使用（b）中报告的相应混淆矩阵所示的测试数据，每层128个滤波器实现了99.16±0.02%的准确率。（c）显示了为区分有助于训练的每个隐藏层的正负训练数据而计算的损失（红线和蓝线），以及训练期间使用的组合损失（绿线）。（d）显示相同隐藏层的辨别精度（红线和蓝线）以及训练期间获得的总精度（绿线）。

在更具挑战性的CIFAR10数据集上，差异开始显现。传统 BP-CNN 的精度约为 85.4%，而 FF-CNN 的表现依赖于标签策略：采用傅里叶波标签时精度为 60.9%，而采用形态学标签时提升至68.6%。这一结果凸显了标签设计的重要性。傅里叶波标签提供了全局一致的信号，但在复杂图像中容易被网络当作“捷径”，导致模型忽视图像本身的细节。而形态学标签通过改变图像结构，迫使网络关注真实的形态特征，从而有效避免了捷径解，提升了分类性能。

在CIFAR100数据集上，研究团队进一步验证了空间扩展标签的可扩展性。通过优化标签集（从 2000 个候选模式中挑选出相关性最低的 100 个组合），FF-CNN 的精度稳定在 37–38%。虽然这一结果仍显著低于 BP 的表现，但它证明了空间标签策略能够在百类任务中保持区分度，具备一定的扩展能力。

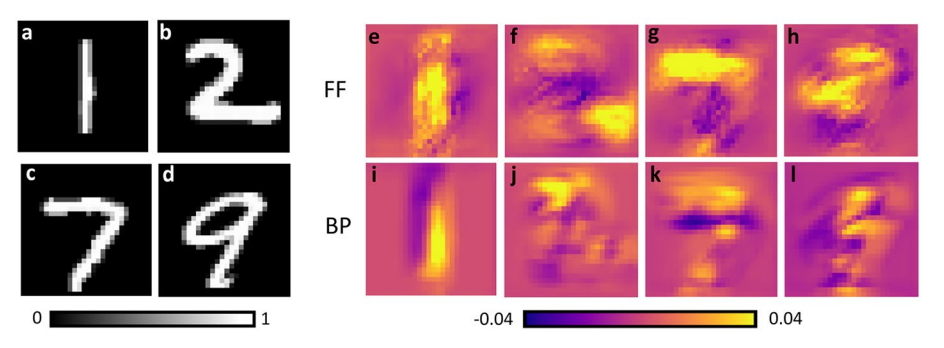
图4：FF和BP训练的CNN的CAM显示了网络在进行预测时认为哪些图像区域是有益的（黄色）或有害的（粉红色）。（a）-（d）显示四个输入图像。（e）-（h）和（i）-（l）分别是基于FF和BP培训的CAM。所有的例子都来自一个每层有16个卷积神经元的网络，滤波器大小为5×5，在200个迭代周期内用50个批量进行训练。FF学习率：5×10^-5，BP学习率：1×10^-3。

整体来看，实验结果揭示了 FF-CNN 的双重特性：在简单数据集上，它能够与 BP 相媲美，并且在硬件资源有限的场景下更具优势；在复杂数据集上，性能依赖于标签策略，形态学标签展现出更强的鲁棒性与合理性。尽管 FF 在精度上仍落后于 BP，但其训练机制的生物学合理性与硬件友好性，使其成为未来类脑计算与低能耗 AI 的潜在候选方案。

这种结果也提示我们，FF 算法的真正价值或许并不在于直接替代 BP，而在于为深度学习提供一种新的思路：通过标签与数据的空间交互，推动网络在前向传播中完成学习。这种理念在未来的 neuromorphic computing（类脑计算）平台上，可能会展现出更大的优势。

05

可解释性与学习动态

在 Forward–Forward (FF) 算法扩展到卷积神经网络的过程中，研究团队特别强调了模型的可解释性与训练动态。这不仅是为了验证 FF-CNN 是否真正学到了有意义的特征，更是为了理解其在复杂数据集上的表现差异。

首先，研究者利用Class Activation Maps (CAMs)对 FF-CNN 的学习过程进行了可视化分析。CAMs 是一种解释性工具，可以揭示网络在做出分类决策时关注的图像区域。实验结果显示，FF-CNN 的不同卷积层往往学习到互补的特征。例如，在识别数字“7”时，某一层可能更关注水平线的内部结构，而另一层则聚焦于边缘轮廓。这种分层互补的特征学习表明，尽管 FF 算法不依赖反向传播，它依然能够逐层构建出有意义的表示，并在整体上形成对图像的全面理解。相比之下，传统 BP-CNN 的特征分布更趋于集中，而 FF-CNN 的特征呈现出更强的多样性和分工性。

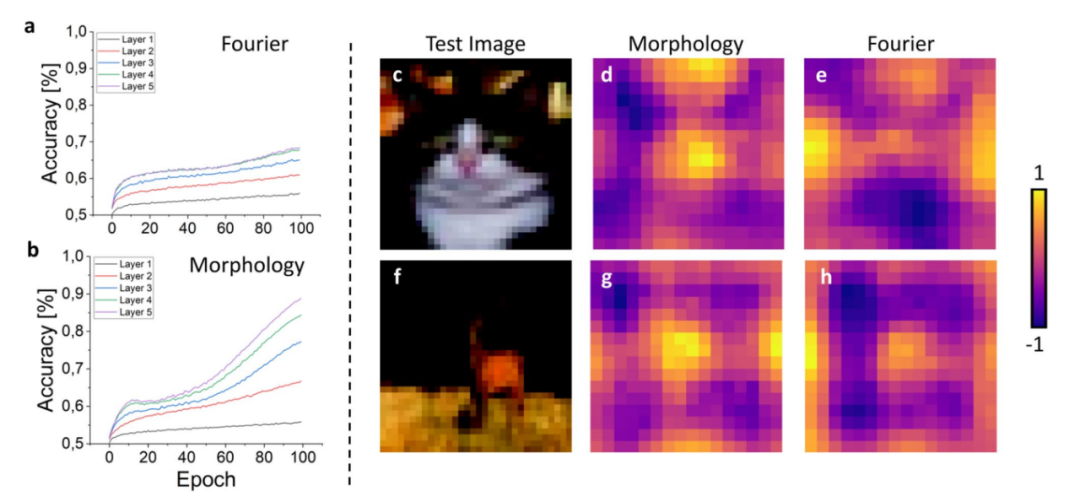
图5：选择不同的空间标签会影响学习过程。（a）和（b）显示了在CIFAR10数据集上测试的FF训练的CNN的隐藏层的二进制精度值（区分正负数据集的能力）。虽然第一层专注于更简单和更粗糙的图像特征，在两种标记策略下表现相似，但深层受益于基于形态学的标记，但当标记是简单的图案时，它们会受到阻碍。给定相同的数据集图像（c）和（f），与基于形态学的标记（d）和（g）相关的归一化CAM产生的最大值主要局限于图像边界（e，h）。

其次，训练稳定性成为 FF-CNN 的一个关键议题。研究发现，FF 算法对标签设计极为敏感。若标签过于简单（如傅里叶波标签），网络可能会走向“捷径解”，即仅依赖标签模式而忽视图像本身的复杂特征；而形态学标签则能迫使网络关注图像结构，从而获得更稳健的收敛路径。这种敏感性意味着 FF-CNN 的训练过程可能出现不同的收敛轨迹，类似于动力系统中的分岔现象：在相同的初始条件下，网络可能因标签设计或参数微小差异而收敛到完全不同的解。

这种分岔特性既是挑战，也是机遇。一方面，它揭示了 FF 算法的非线性与复杂性，说明其学习动态比传统 BP 更难以预测和控制；另一方面，它也为研究类脑学习提供了新的视角——生物神经系统的学习过程本身就充满不确定性和多样性，FF 算法的这种特性或许更接近真实的神经学习机制。

综上，FF-CNN 的可解释性分析表明，它能够在不同层次上学习互补特征，而训练动态的分岔现象则提醒我们，标签设计与参数选择在这一框架下至关重要。这不仅是技术上的挑战，更是理解类脑学习与人工智能之间关系的重要窗口。

06

应用前景与挑战

Forward–Forward (FF) 算法在卷积神经网络中的扩展，展示了其独特的应用潜力。首先，它的最大优势在于 局部更新与低内存需求。与反向传播需要存储大量中间激活值不同，FF 算法只依赖局部的 goodness 函数进行权重更新，这使得训练过程更加轻量化，尤其适合在显存有限或硬件受限的环境中运行。

其次，FF 算法的机制天然契合 类脑硬件的实现。在 neuromorphic computing（类脑计算）平台上，反向传播往往难以实现，而 FF 的双前向传播与局部更新则更接近生物神经系统的学习方式。这意味着 FF-CNN 有望成为未来低能耗硬件和类脑芯片上的重要候选算法。

此外，FF 算法本身就是一种 生物学启发的学习机制。它通过正负样本的对比来驱动学习，类似于神经系统在强化与抑制之间的动态平衡。这种机制不仅为人工智能提供了新的训练思路，也为理解人类大脑的学习过程提供了可能的模型。

然而，挑战同样显而易见。首先，FF 的 推理计算开销较大。在 goodness 比较模式下，每个输入需要与所有可能的标签组合进行前向传播，这在多类别任务中会显著增加计算量。其次，FF 算法的 理论收敛性尚未严格证明，其训练动态存在分岔现象，意味着结果可能因标签设计或参数微小差异而大幅不同。最后，在复杂数据集上，FF-CNN 的表现仍明显落后于 BP-CNN，尤其是在 CIFAR10 和 CIFAR100 上，精度差距较大。这表明 FF 算法在实际应用中仍需进一步优化。

07

结论与展望

综合来看，本文的研究证明了FF 算法在 CNN 中的可行性。通过空间扩展标签策略，研究团队解决了卷积核无法捕捉局部标签信息的问题，使得 FF-CNN 能够在图像任务中实现有效训练。这一创新不仅是技术上的突破，更是理念上的转变：它强调在前向传播中完成学习，而非依赖反向传播的链式梯度。

展望未来，FF 算法的应用潜力主要集中在三个方向。首先是类脑硬件，在neuromorphic 芯片和低能耗计算平台上，FF 的局部更新机制可能展现出更大的优势。其次是无监督学习，FF 的正负样本对比机制天然适合在缺乏标签的场景中进行特征学习。再次是 对比学习，通过扩展正负样本的构造方式，FF 有望与现代自监督学习方法结合，提升在复杂任务中的表现。

更深层的意义在于，FF 算法为深度学习提供了一条 生物学启发的替代路径。它不仅是对反向传播的技术挑战，更是推动人工智能与神经科学交叉发展的桥梁。随着研究的深入，我们或许能够在 FF 框架下找到更接近人脑学习机制的算法，从而为智能计算开辟新的方向。

这项研究提醒我们，深度学习的未来不止于更大的模型和更强的算力，还可能在于更接近生物本质的学习方式。Forward–Forward 算法正是这一探索的重要一步。（END）

参考资料：https://www.nature.com/articles/s41598-025-26235-2